
I think functional programming (FP) has become a necessary skill to have for any software developer or programmer in general. Considering the tools used in industry today, like React.js, Elm, and all the popular functional languages, you don’t want to miss out on all the awesomeness. Despite the fact that you need a certain level of understanding of functional programming in order to be proficient in use of these tools, understanding of the general concepts of FP can make you a much better software developer in general. Plus, a lot of frameworks and programming languages that aren’t considered functional actually have functional features. Python, JavaScript, Java, C#, Dart, and many other languages have quality of life functional features that can save you a lot of time and headache if you know how to use them properly.
If you look carefully at these tools, you notice a lot of underlying concepts that are common to all of them. Having a solid understanding of the fundamentals on which these tools were built can carry you much of the way towards mastering them, and certainly makes your life easier when learning to use new tools (and judging them.)
In this article, I attempt to explain the basics of FP using Haskell. Don’t worry if that sounds scary, it’s really simple stuff.
Functions!
If you squint hard at any computer program, you notice that it’s essentially the following:
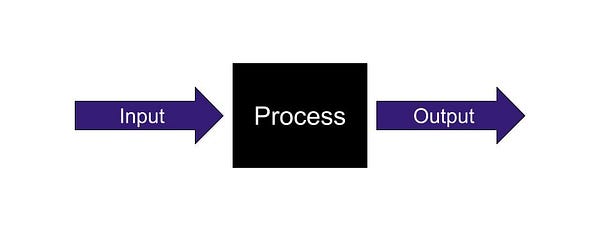
It’s a process that you feed data, and outputs something. The input can be anything from user clicks, to command line arguments, and the output can be a file, or search results.
There’s a really simple way to express this notion of transforming input to output: mathematical functions. If you already have a good understanding of functions, I can understand why you might be skeptical of the idea that any program can be modeled as a mathematical function. You’re right, a function can’t be used to model writing a file to disk. However, functions are the simplest way to model data transformations, which make up most of our programs..
You may have learned about functions in programming. When I’m talking about functions, I do not mean “customizable and reusable pieces of code.” What I mean is way simpler than to print something to the screen, or to change the value of some variable outside of it. If you’re not familiar with mathematical functions, let me explain.
A function in mathematics is a relation between two sets A and B, such that every element in A is associated with one and only one element of B. Sounds complicated? This might help:
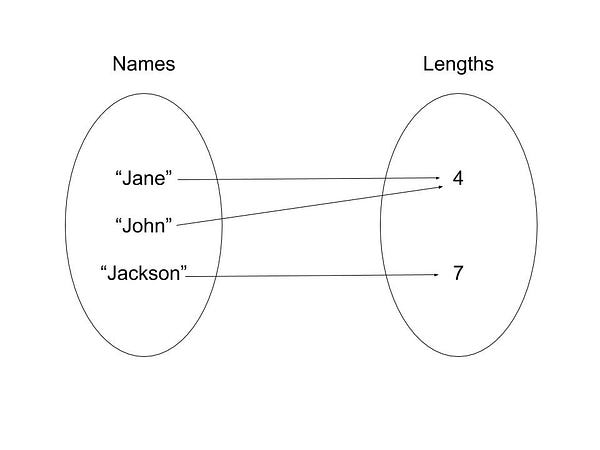
In essence, a set is a collection of unique elements. In this example, we have two sets: Names (with a capital N,) and Lengths (with a capital L.) These two sets are related in the sense that every name has a length (the number of characters in it.) Since every name is associated with only one length, we can call this relation a mathematical function. Let’s call this function length.
Functions can be thought of as mappings between elements of sets. In length, the element “John” is mapped to 4. We note this mapping as length(“John”)=4, which in plain English translates to: length of “John” equals 4. We can also say that applying length to “John” yields 4.
A value passed to a function as input is called an argument of the function. When a function is applied to an argument, the result is called the image of that argument, and the argument itself is called the preimage . In length, the image of “Jane” is 4.
Notice how the mapping has a direction: it goes from Names to Lengths. More generally, we call the “original” set the domain of the function, and the set to which the elements of the domain are mapped the co-domain. For length, the domain is the set Names, and the co-domain is the set Lengths.
You can type the expression length("John") into this Haskell REPL to the right and hit Enter to get the result. A REPL is just a program that reads, evaluates, and prints the result of expressions you give it. Feel free to try running any code you see in this article.
Any function can be expressed as a set of pairs. Each pair in this set consists of a value from the domain, and its corresponding image in the co-domain. Our little length function can be expressed as:
[("Jane", 4), ("John", 4), ("Jackson", 7)]where all the elements between the brackets ([]) form a set. In programming (inconveniently,) it is not necessarily the case that all the pairs that form a function are known before executing it. Imagine a function from the infinite set of integers (ℤ) to the infinite set of real numbers (ℝ.) How can we possibly fit all the pairs that form this function in the finite memory of a computer? Stay tuned.
I guess it’s appropriate now that I define functional programming. FP is using mathematical functions as the primary building block of programs. In other programming paradigms, the primary building block would be instructions, or objects. Using functions instead gives you some superpowers that are beyond the scope of this article, but they’re very simple, which is a huge plus.
Equations
Earlier I implied that in programming, we normally don’t know all the pairs of preimages and images that form a function. Most of the time, we can’t even write these pairs down because there are so many (possibly infinitely many.) Consider a function that maps an integer to its increment (the number + 1.) This function is impossible to write out as a set of pairs because the integers never end.
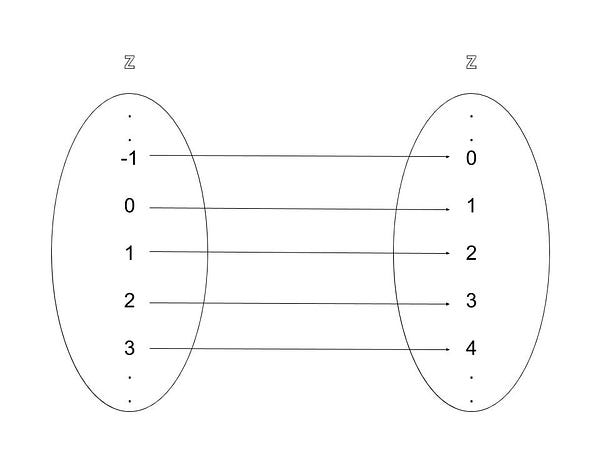
In such cases, we can express the function as an equation. A formula that the computer can use to compute the image of a given argument. In the case of our increment function, writing the equation isn’t very difficult:
increment(x) = x + 1This equation is read: “the increment of x is equal to x + 1.” Isn’t it wonderful! Instead of writing out the mapping with concrete arguments in this form:
increment(1) = 2
increment(2) = 3
increment(3) = 4
...We can generalize the formula to work with any given integer by making the argument’s value unknown in the equation, making it a parameter. The image of a particular value can be computed by applying the function:
increment(60)This expression will yield 61 (the image of 60.)
In Haskell, you actually don’t need parentheses in function definitions and applications. You can use spaces instead:
increment x = x + 1
increment 60We can call function definitions equations in Haskell because the two sides are literally equal. You can take out any application of a function and put the evaluated right-hand side of the function equation in its place, and you would get exactly the same result. The same can be said for any Haskell expression. Think of it as being able to take out 250 * 2 and placing 500 instead of it. This property is known as referential transparency, and it just makes programs much easier to think about_._
Function Types
Remember what I said about mapping having a direction? Let’s take a closer look at our increment function. It is a function that maps the elements of the set of integers (ℤ) to the set of integers + 1 (also ℤ.) In mathematics, this direction is noted as ℤ ↦ ℤ. In Haskell, we think a lot about the types (basically sets)of data that we operate on. There are many predefined sets already built into the language, such as Int for integers, Float for floating-point numbers, Bool for True and False, and String for text. But functions have types of their own. A function going from integers to integers has the type Int -> Int.
When defining a function, it is almost never necessary to explicitly specify its type. The Haskell compiler can figure the type of the function on its own by looking at how the function’s parameters are being used. Adding type annotations makes it easier for you to just look at the function’s name and type (its signature) and immediately have a good idea of what it does.
The definition of increment with explicit type annotations is as follows:
increment :: Int -> Int; increment x = x + 1Now you can read this definition as: “increment is a function from Int to Int; the increment of an integer x equals x + 1.”
When writing Haskell code in a file (not in the REPL,) you can write the type annotation on one line, and the actual function definition on the next line. This makes it possible to omit the semicolon (;.)
Looking at our definition of increment with the eyes of a lazy programmer, I can see a small problem: it can only be used to increment integers. Wouldn’t it be great if the function could be applied to arguments of any numeric type? It would make sense for us to use the same function to increment floating-point numbers too, right? Coming soon.
Functions of Multiple Parameters
Let’s say we want to define a function f that takes two integer parameters: x and y. The function squares x and adds it to y. This is how it would look in Haskell:
f x y = x * x + ySimple enough. Now you can apply f to two space-separated arguments:
f 2 3which yields 7. Great! Now on to the weird part.
If we were to redefine f with type annotations, it would look like this:
f :: Int -> Int -> Int; f x y = x * x + yThat’s strange… Look at the type of f… It’s Int -> Int -> Int! Why is that? Shouldn’t it be (Int, Int) -> Int since it takes a pair of integers and maps them to a single integer? And what does it mean to have two arrows in a function’s type anyway?
This weirdness is a consequence of a concept called currying, which I’ll explain when it becomes useful.
Let’s take a break from types for now. In order for the rest of the concepts I’d like to explain to make sense and feel useful, I feel it is appropriate to take a look at a very important data structure first: the list.
Lists
When you have a number of related data points that you would like to process together, it’s a good idea to store them in some sort of container that preserves their structure, and gives you some tools to help with your processing task. Lists are great data structures that do just that. They can be used to store data in an ordered manner, in the sense that the first element in the list comes before the second element, and the second comes before the third, and so on. Lists also let you easily walk through all the elements within them, transform them, filter them, and aggregate them.
Let’s define a list of the integers from 1 to 5 and name it oneToFive:
oneToFive :: [Int]; oneToFive = [1,2,3,4,5]You’ll notice that the type of oneToFive is [Int] (read “list of Int.”) We can construct lists by using square brackets ([]) to surround the comma-separated elements of the list. This is awesome! Let’s see what we can do with this list.
In Haskell, there are lots of predefined functions that operate on lists. One of these functions is head, which maps a list to its first element. For instance:
head oneToFivewould yield 1 (the first element of [1,2,3,4,5].) Another function is tail, which maps a list to its self, but without the head:
tail oneToFivewill yield [2,3,4,5](oneToFive without 1, the first element.) A list can be pictured as a snake, even though this is not a perfect analogy — snakes can’t regrow their heads:
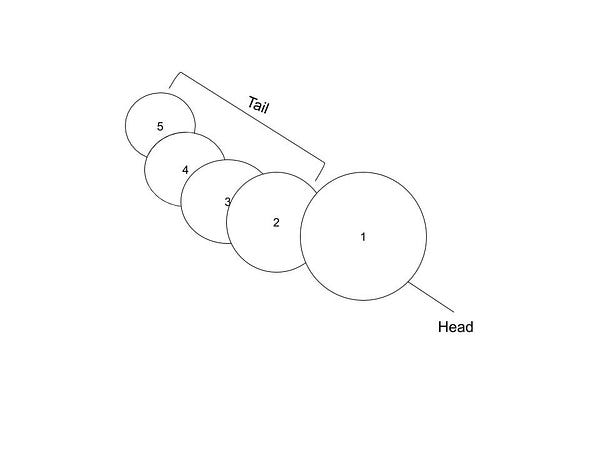
Take the list’s head, and you’re left with its tail. A list’s tail is a list itself, so it has a head and a tail. Take the list’s tail’s head, and you have the second element (2.) Take the list’s tail’s tail’s tail’s tail’s head, and you’ll get 5:
head(tail(tail(tail(tail(oneToFive)))))How fun. What about the head of an empty list? Well, it doesn’t exist, so you can’t get it. The same goes for the tail of an empty list. Now, let us think for a moment about the tail of a list with one element. That’s tricky, but let’s reason about it this way:
If we have a list of five elements, then its tail should have 4 elements (5 minus the head.) So we can say that the length of the tail is the length of the whole list minus one. But it doesn’t make sense for a list to have a length less than 0 (being empty,) so the base case, or the most basic case for a list, is to be empty. So it makes sense for the smallest possible tail to be the empty list.
Other than using square brackets to construct lists, you can use the colon operator (:, a.k.a. the construction operator) to stick a head to a tail, therefore constructing a new list. For example, oneToFive can be defined as:
oneToFive = 1:2:3:4:5:[]The expression is evaluated from right to left. We’re sticking 5 to [], 4 to [5], 3 to [4,5], 2 to [3,4,5], and 1 to [2,3,4,5], thus getting [1,2,3,4,5]. Using this notation, it’s clear how the smallest possible tail of any list is the empty list ([].) Without it, you wouldn’t be able to construct any list, because you wouldn’t be able to “end the cycle.” This brings us to a very important concept in functional programming: recursion.
Recursion
A list can either be empty ([],) or it can consist of an element x stuck to the beginning of a list (x : aList.) Do you notice anything weird about this definition of a list? We’re defining a list in terms of its self. It makes complete sense when you think about it. There are only two possible ways a list can exist: either as the empty list, or as a construction of a head and a tail list. The key here is that in a construction of a head and tail, the tail can be any list, either empty, or a construction of its own.
Let’s try to define a function that maps a list to the count of its elements. Let’s call it count.
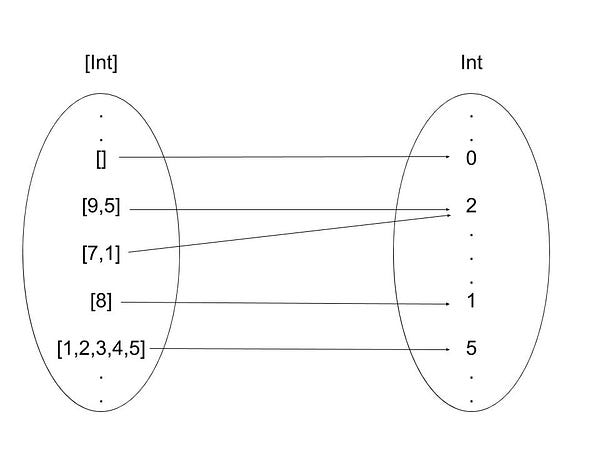
This function should have one parameter: the list of elements we want to count. A list can either be empty, or a construction of at least one element (a head,) and a tail. These are the only two cases we have to deal with since the function only has one parameter, which is a list.
The first case is that of an empty list. Easy, an empty list has zero elements:
count [] = 0The second case is that of a construction. Hmm… A construction consists of a head (1 element,) and a tail (a list of unknown number of elements.) Ok, so the count of the elements in a construction is 1 + the count of the elements of the tail. Wait… Let’s write that down:
count (h : t) = 1 + count(t)where h is the head, and t is the tail. Together with the empty list case, the whole definition would be:
count [] = 0; count (h : t) = 1 + count(t)Now that’s just magical. If what’s going on is not obvious, maybe this will help:
Earlier I explained how functions are equations. We can use this fact to understand how count works by applying it to some list (e.g. oneToFive,) and walking through the evaluation of the result one step at a time.
count [1,2,3,4,5] = 1 + count([2,3,4,5])
count [1,2,3,4,5] = 1 + (1 + count([3,4,5]))
count [1,2,3,4,5] = 1 + (1 + (1 + count([4,5])))
count [1,2,3,4,5] = 1 + (1 + (1 + (1 + count([5]))))
count [1,2,3,4,5] = 1 + (1 + (1 + (1 + (1 + count([]))))))
count [1,2,3,4,5] = 1 + (1 + (1 + (1 + (1 + 0)))))
count [1,2,3,4,5] = 1 + 1 + 1 + 1 + 1 + 0
count [1,2,3,4,5] = 5Again, notice how the evaluation would never have ended successfully without a base case (count [].)
In general, recursion is defining something in terms of its self. Data structures can be recursive; functions can be recursive; relations in general can be recursive. You’ll find that thinking recursively can make things a lot simpler sometimes.
You may have learned about loops in programming (e.g. for and while loops,) and you may be wondering why you would ever use recursion. Well, one reason is that Haskell and some other functional languages don’t have any looping constructs built into them. Another reason is that using recursion lets you use the equational reasoning we applied earlier when evaluating count(oneToFive) in all sorts of situations, saving you some brain power. Most importantly, though, I think recursion makes it easy to describe things clearly and concisely, which results in more understandable code.
Higher-Order Functions
Yet another scary term.
Let’s imagine a scenario where you have a list of integers, and you want to increment each of them. You define a function incrementAll that does just that:
incrementAll [] = []; incrementAll (h : t) = h + 1 : incrementAll tEasy. To increment all the elements of an empty list, you do nothing with it. To increment all the elements of a construction, you increment its head, and stick it to all the incremented elements of the tail. Great. You later require a function to decrement all the integers in a list, so you define decrementAll:
decrementAll [] = []; decrementAll (h : t) = h -1 : decrementAll tLater, you require another function to multiply the integers by two, so you define doubleAll:
doubleAll [] = []; doubleAll (h : t) = h * 2 : doubleAll t… There’s a problem here. We’re duplicating a lot of code, which quickly becomes boring. If you look at these three functions, you notice they’re essentially the same function, but they map the elements of the list differently. All three walk through the list recursively, and transform its elements using some function (e.g. increment.) How do we solve this problem?
Remember what I said about functions having types of their own? Functions can be divided into sets. There’s the set of functions from integers to integers (Int -> Int,) the set of functions from lists of integers to integers ([Int] -> Int,) and so on. We can think about a function as we would an integer; we can pass an integer as an argument to a function, right? Why not do the same with functions?
Let’s define a function transform that walks through a list, and transforms each element using a function f that we pass as an argument:
transform f [] = []; transform f (h : t) = f(h) : transform f tLooks awfully similar to the previous functions, but with the extra parameter f. What we’re doing here is that we’re leaving the function used to transform the elements up to the user of transform. All we do in transform is traverse a list, and apply a given function f to its elements. Let’s try using it with increment and oneToFive:
transform increment oneToFiveyields [2,3,4,5,6]. Awesome! Note that increment and oneToFive are both arguments of transform. We are not applying increment to oneToFive. Now let’s try transform with decrement:
decrement x = x - 1
transform decrement oneToFiveyields [0,1,2,3,4]. It works! We can do the same with doouble, but you get the point. transform can be used with any function as long as its type is compatible with the type of the elements of the list.
A higher-order function is simply a function that takes a function as an argument. So transform is a higher-order function. Many of these functions are available in Haskell by default. For example, filter can be used to filter a list:
filter even oneToFiveThis will filter the even numbers in oneToFive and yield [2,4]. even is a simple function that takes an integer, and yields True if it’s even, and False if it isn’t. The filter function uses the function you pass it to test the elements of the list, and keeps the elements that pass the test.
Another popular function is foldl (short for “fold left,”) which “folds” a list as if folding a long piece of cardboard starting from the left and reducing it to a small piece. For example, we can use foldl to find the sum of all the elements of a list of integers:
foldl (+) 0 oneToFiveyields 15. foldl takes three arguments: the function used to calculate the result of every fold, the initial value to start folding with, and the list to fold. This is a bit abstract. If you know about for loops, you can think of folds as loop iterations, where in each iteration, you change the value of some accumulator. In the case of folding a list of integers to find their sum, the accumulator would be the sum, which starts at zero, and then increases with every number you pass in the list to finally be returned as the sum of all the numbers in the list.
Notice there’s something peculiar about the function we passed to foldl. As the function used to calculate the accumulator in each fold, we used (+). This is possible because operators in Haskell are really just functions of two parameters. To multiply two integers, you pass them as arguments to the (*) function:
2 * 4
(*) 2 4both yield 8.
Higher-order functions aren’t limited to lists. They can be used in all sorts of situations (e.g. asynchronous programming,) and they are a good tool for abstraction. We can generalize a formula by making some part of it unknown, and allowing it to be passed as an argument.
We’ve gone through many concepts so far. We’ve built a pretty good intuition about functions, and we’ve seen how powerful they are. We’ve also discussed types briefly, but now I’d like you to run these lines in the REPL:
f :: Int -> Int -> Int; f x y = x * x + y
:t f
:t (f 2)
:t (+)
:t (1+)
:t length
:t mapTake a quick look at the result of each of these. :t is a command you can use in the REPL to get the type of an expression. But what’s with these types? There are lots of a’s and fat arrows (=>.) What do they mean? And the question about multiple arrows in the types of functions of multiple parameters remains unanswered! What have we been doing all this time!
Currying
The result of :t f is Int -> Int -> Int, which is strange. The result of :t (f 2) is Int -> Int, which is even stranger. Doesn’t f take two arguments? Well, that’s the key: f takes two arguments, but (f 2) is another function that takes only one:
f 2 3
(f 2) 3both yield 7. You can even assign a name to (f 2):
g = (f 2)Now g is a function just like (f 2). It takes one integer argument, and yields an integer, so g 3 will yield 7. Since we’re applying f to only one argument, the value we provide will be used in place of the first parameter (x.) The resulting function takes the one remaining argument (y,) and finally yields an integer.
Currying (named after Haskell Curry) is making a function yield another function when it’s not applied to enough arguments. If a curried function takes 5 arguments, applying it to 3 arguments will yield a function that takes 2 arguments. In Haskell, all functions are curried, which allows us to write more concise code. For example, instead of writing a function that sums the elements of a list as:
sum list = foldl (+) 0 listwe can just write:
sum = foldl (+) 0Since foldl takes 3 arguments, and we’re applying it to 2 arguments, it will yield a function that takes one argument (the last parameter, a list,) and finally yields the sum.
Another example would be to use curried functions as arguments to higher-order functions. Remember transform? There’s actually a function just like it already defined called map that transforms every element of a list using some function you pass:
increment x = x + 1
map increment oneToFivewill yield [2,3,4,5,6]. The addition operator is a function, though, and all functions are curried. So we can apply (+) to one argument, and get a function that takes one argument. So increment can be rewritten as:
increment = (+1)which is cool. But now we don’t really need increment since we have a clear simple way to get a function that increments a number. So a function incrementAll that increments all the elements in a list can be written as:
incrementAll = map (+1)This works because map has two parameters (a function and a list,) and we’re only applying it to one argument. This is just beautiful.
Alright, we’ve discovered the secret of functions of multiple parameters. Now, let’s answer the question about all the a’s and b’s in types like :t map:
map :: (a -> b) -> [a] -> [b]Parametric Polymorphism
What a tongue twister.
In previous sections, we looked at cases where you can generalize a definition by making some part of it unknown. Types are no different; if you take a look at the list type [] you might notice that it’s missing something: the type of elements within it. In order to create a list, you must make it a list of something, so you can think of the list type as a function on the type level that has a type parameter. So to construct a list type that has elements in it, you must pass some type to []. The type [Int] is Int passed to [] as an argument. Because [] itself isn’t a complete type and it has a type parameter, it is called a type constructor.
Because a list can come in many forms (e.g. [Int], [Float], and [String],) we say it’s polymorphic. Since the type argument is the part that varies among lists, we say it’s parametrically polymorphic.
The same idea applies to functions; in :t map, the type of the list doesn’t matter, because the operations we perform on the list require no knowledge of the type. That is why you see [a] and [b] in :t map. Both a and b can vary between different applications of map, which is why they’re called type variables, and map is called a polymorphic function. For example:
map (+1) oneToFiveHere, a is Int, and b is Int. So map has the type:
map :: (Int -> Int) -> [Int] -> [Int]This also shows that a and b are not necessarily different types. Here’s another example:
names = ["John", "Jane", "Jackson"]
map length namesHere a is String, and b is Int. So the type of map is:
map :: (String -> Int) -> [String] -> [Int]This polymorphism becomes really useful when you want a function or a type to work with multiple types. If you were defining a list data structure, you shouldn’t care about the type it’ll be used with, because you would want it to be usable with any type. It’s also great that the Haskell compiler can figure out types on its own, so you don’t need to think about it too much. Simply define a function, and look at the type that the compiler has given to it, it’s usually the most generic type possible.
Type Classes
Check out the type of (+):
(+) :: Num a => a -> a -> aOk, we understand from a -> a -> a that it’s a function that takes two a’s and yields an a. But what’s with the Num a => at the beginning?
Imagine you’re defining the (+) function. Would you want it to be usable with any type? I think not. You would want (+) to be usable with types that have properties of numbers (or I hope so, at least.) That’s what the Num a is for. It limits a to types that are number-like. But what is Num?
In order for something to be number-like, it has to support some operations like addition (+,) multiplication (*,) and a few others. If a type can be operated on using these functions, we consider it number-like.
In Haskell, you can define a type class containing the specification of functions that a type needs to support in order to be considered a member of some class of types.
The definition of the Num type class looks like this:
class Num a where
(+), (-), (*) :: a -> a -> a
negate :: a -> a
abs :: a -> a
signum :: a -> a
fromInteger :: Integer -> a
x - y = x + negate y
negate x = 0 - xSome of the functions every Num has to support aren’t concretely defined inside the type class. Functions like (*) and abs are left up to the author of a to define, so only their types are specified. Other functions like (-) have a default concrete definition, given by x — y = x + negate y, so the author of a needs only to define negate for (-) to become available.
Let’s define our own type class called FillStatus. Any member type of FillStatus must support a function isEmpty that tells us whether the argument is empty or not:
class FillStatus a where isEmpty :: a -> BoolSo isEmpty takes an a and returns a Bool (True or False.) Now let’s make lists satisfy the requirements of FillStatus by defining an instance of FillStatus for [a]:
instance FillStatus [a] where isEmpty [] = True; isEmpty _ = FalseThe definition of isEmpty for lists is pretty straightforward: a list is empty if it’s the empty list ([]) and it’s not otherwise (that’s what the underscore means.) Awesome! Now isEmpty [] yields True, and isEmpty [1,2,3] yields False!
We can provide an instance of FillStatus for any type we want (as long as it makes sense.) Type classes are similar to interfaces in other programming languages like Java, but there’s a key difference between the two: you don’t need to specify which type classes a type belongs to while defining it. Int is already defined, and we can still create an instance of FillStatus Int without modifying the definition of Int.
Conclusion
We’ve looked at many functional programming concepts in this article. However, this is by no means a comprehensive explanation of FP or Hakell. It is an introduction and a quick overview. After understanding the contents of this article, you should be able to read a lot of Haskell code, and write code in a functional way. I haven’t mentioned things like state, Haskell’s relationship with category theory , or even fundamental things like anonymous functions because this article is long as it is. But I’ll be writing more in the future.